PORADNIK NDN

Czy warto inwestować w mierniki z przetwornikiem True RMS?

O wyborze cyfrowego miernika uniwersalnego decyduje szereg czynników. Z pewnością do najważniejszych należy cena, ale jest ona tylko pochodną parametrów technicznych. O jakości przyrządu decyduje jego dokładność i rozdzielczość, a także zakresy, funkcje pomiarowe oraz typ zastosowanego przetwornika.

Multimetry z przetwornikami True RMS są w powszechnej opinii uznawane za znacząco droższe od mierników z przetwornikami RMS. To, jak „znacząca” jest to różnica łatwo można sprawdzić przeglądając ceny na stronach internetowych dystrybutorów. W artykule rozpatrzymy przyrządy firmy Sanwa, których dystrybutorem jest firma NDN ( http://www.ndn.com.pl/ ).
Jak łatwo się przekonać, różnica cen mierników True RMS i RMS produkowanych przez firmę Sanwa chociaż faktycznie istnieje, e rzeczywistości nie jest na tyle duża, aby w ogóle zastanawiać się nad wyborem. Tak czy inaczej, warto mieć świadomość różnic występujących pomiędzy obydwoma typami mierników.

Definicja wartości skutecznej napięcia

Rys. 1. Równoważne obwody stało- i zmiennoprądowe

Aby zrozumieć na czym polega różnica pomiędzy miernikami RMS i True RMS konieczne jest przypomnienie definicji napięcia skutecznego. Wyobraźmy więc sobie, że mamy źródło napięcia stałego UDC i dołączony do niego odbiornik, np. rezystor o rezystancji R (rys. 1). Na skutek przepływającego prądu wydzieli się w nim moc P=U²/R=I²*R. Teraz rozpatrzymy obwód ze źródłem napięcia przemiennego, np. sinusoidalnego. Jeśli jego amplitudę ustalimy tak, aby w odbiorniku wydzieliła się taka sama moc, jak w pierwszym przypadku, mówimy że napięcie skuteczne drugiego źródła jest równe napięciu źródła pierwszego. Z fizycznego punktu widzenia podstawowymi parametrami sygnału sinusoidalnego są: amplituda (nie wartość skuteczna) i częstotliwość. W elektronice jednak dużo wygodniejsze jest stosowanie pojęcia napięcia skutecznego. Dla sygnału sinusoidalnego zależność między amplitudą a wartością skuteczną określa wyrażenie:

(1)

gdzie: Um – amplituda sygnału sinusoidalnego
URMS – napięcie skuteczne.
Należy zwrócić uwagę na to, że dla każdego innego sygnału zależność (1) będzie ulegała zmianie. Wróćmy do mierników, zwracając szczególną uwagę na zasadę ich działania. Cofnijmy się na chwilę do epoki multimetrów wskazówkowych z ustrojem magnetoelektrycznym. Przyrządy te na napięciowych zakresach zmiennoprądowych mierzyły z zasady działania wartości średnie wyprostowane, ale dla wygody użytkowników były skalowane na wartości skuteczne. Wartość średnia wyprostowana przebiegu sinusoidalnego jest równa

(2)

stąd zależność między napięciem skutecznym a średnim jest wyrażona zależnością:

(3)

O taki współczynnik wymnażane są zatem wskazania mierników mierzących w rzeczywistości wartości średnie wyprostowane, a podających wartości skuteczne. Dotyczy to nie tylko mierników z ustrojem magnetoelektrycznym. Mierniki cyfrowe z przetwornikami RMS wykonują tę samą operację. Wszystkie podane na wstępie zależności są dla nich słuszne, ale tylko dla napięć sinusoidalnych. Zmiana kształtu napięcia spowoduje nieuchronną zmianę wskazań miernika, co wynika ze zmiany funkcji podcałkowej w wyrażeniu (2) oraz stosowania przelicznika dla sygnału sinusoidalnego. Z problemem tym nie poradzą sobie zwykłe mierniki RMS. Pomiary wykonane miernikami z przetwornikiem True RMS będą prawidłowe, gdyż wykonują one całkowanie przebiegu zgodnie z definicją napięcia skutecznego podaną w wyrażeniu (4). Uniezależniają się więc od kształtu mierzonego sygnału, ale pozostaje problem składowej stałej.

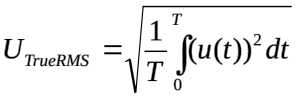
(4)

Duża część multimetrów cyfrowych, może nawet większość, mierzy napięcie skuteczne bez składowej stałej (UACRMS). Taki pomiar funkcjonalnie odpowiada pomiarom wykonywanym miernikiem RMS, w którym z zasady działania eliminowana jest składowa stała. Napięcie skuteczne mierzone przyrządem True RMS na zakresie zmiennoprądowym (oznaczenie V z falką) jest więc w rzeczywistości prowadzone z zastosowaniem wyrażenia (5):

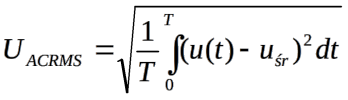
(5)

w którym:

(6)

Można więc uznać, że stwierdzenie iż mierzą one napięcie True RMS jest w odniesieniu do takich miernikach pewnym nadużyciem, gdyż wprawdzie mierzą one prawidłowo sygnał niezależnie od jego kształtu, ale nie uwzględniają składowej stałej. Wynik nie jest więc zgodny z definicją wartości skutecznej. Tak podane napięcie nie zapewnia energetycznej równoważności między obwodami stało- i zmiennoprądowymi, o których była mowa na wstępie artykułu. Nie oznacza to jednak, że pełnego pomiaru wartości skutecznej nie można wykonać miernikiem True RMS eliminującym składową stałą. Konieczne jest jednak wykonanie dwóch kroków. W pierwszym mierzymy napięcie na zakresie stałoprądowym (otrzymujemy UDC=Uśr), w drugim natomiast mierzymy składową UAC na zakresie zmiennoprądowym. Ostatecznie pełne napięcie skuteczne jest równe: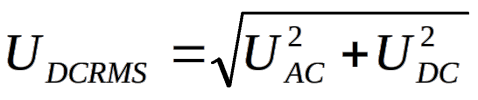


Przeliczenia takiego nie trzeba wykonywać korzystając z mierników mających zakres oznaczany np. jako AC+DC. Przykładem jest multimetr Sanwa PC7000.
Należy jeszcze dodać, że chociaż w rozważaniach były rozpatrywane napięcia, to wszystkie wnioski są oczywiście słuszne również dla prądów.

Ostateczna decyzja: RMS czy True RMS?
Czytelnicy, którzy niechętnie czytają rozważania teoretyczne oczekują zapewne wniosków praktycznych. Na czym zatem polega wyższość mierników True RMS nad miernikami RMS? To już wiemy. Pomiary sygnałów niesinusoidalnych, zwłaszcza impulsowych, miernikiem RMS, na pewno będą obarczone dodatkowym błędem nie podawanym w specyfikacji przyrządu. Co więcej, w większości przypadków błąd ten będzie trudny, albo wręcz niemożliwy do wyznaczenia. Miernik RMS będzie więc raczej nieprzydatny dla elektroników zajmujących się wszelkiego rodzaju układami impulsowymi – przetwornicami, falownikami itp. Problem polega na tym, że współczesna elektronika w coraz większym stopniu jest oparta właśnie na technice impulsowej. Szukać nie trzeba daleko – rozpatrzmy choćby pomiar prądu pobieranego przez powszechnie stosowane żarówki energooszczędne. Jeśli zostanie on wykonany miernikiem RMS, wynik będzie obarczony tak dużym błędem, że trzeba go będzie uznać za zupełnie bezużyteczny.
No dobrze, mamy świadomość błędów popełnianych podczas pomiarów sygnałów niesinusoidalnych miernikiem RMS, ale może nie są one tak duże, aby nie można ich było zaakceptować. Rozważmy przykład pomiaru napięcia prostokątnego o współczynniku wypełnienia 0,5 miernikiem Sanwa CD771. Maksymalny błąd pomiaru na zakresie AC jest według specyfikacji określony jako ±(1,2% rdg + 7 dgt), gdzie rdg – wartość czytana, a 7 dgt oznacza odchyłkę wskazania na najmniej znaczącej pozycji. Załóżmy, że mierzone jest napięcie równe 1,000 V. Bezwzględny, maksymalny błąd pomiaru jest więc równy:
ΔU=±(0,012*1,000+0,007)= ±0,019 V
Tymczasem samo skalowanie przebiegu prostokątnego o wypełnieniu 0,5 stosowane w mierniku RMS daje około 11-procentowy błąd. W powyższym przykładzie będzie to odpowiadało napięciu 0,11 V. Czy jest to wartość do zaakceptowania? Odpowiedź pozostawiam czytelnikom do własnej oceny. Trzeba jeszcze pamiętać, że błąd pomiaru będzie się zwiększał tym bardziej, im współczynnik wypełnienia przebiegu prostokątnego będzie się różnił od wartości 0,5. Wniosek wypływający z tej analizy może być tylko jeden: do pomiarów przebiegów o charakterze impulsowym mierniki RMS zupełnie się nie nadają. Przykładem niech będzie pomiar prądu pobieranego przez popularną żarówkę energooszczędną. Na fot. 2 przedstawiono porównanie pomiarów przeprowadzonych miernikami RMS (pierwszy od lewej) i True RMS.

Fot. 2. Pomiar prądu pobieranego przez żarówkę energooszczędną przeprowadzony miernikami RMS (pierwszy od lewej) i True RMS

PREZENTACJA WIDEO